Apuntes de electrónica: Condensadores

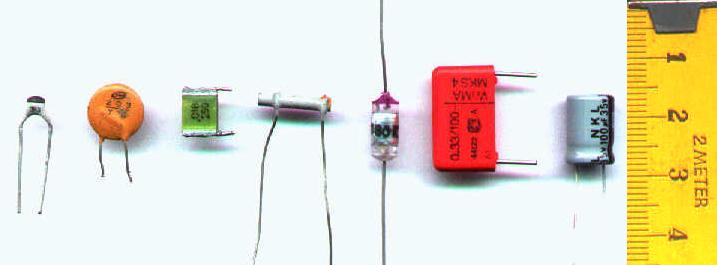
Los condensadores son los dispositivos electrónicos más sencillos. Esta afirmación se sustenta en que cualquier niño es capaz de fabricar un condensador en casa.

Taller para niños: fabrica tu propio condensador

Para fabricar nuestro propio condensador necesitamos los siguientes materiales:

• Papel de aluminio (el de los bocatas)
• Cualquier lámina de material aislante (dieléctrico): papel (folios), papel de horno, cartulina…
• Pegamento: cola blanca o similar adecuado para trabajar con niños

El proceso es muy sencillo:

1. Recortamos dos cuadrados de papel de aluminio de aproximadamente 5 centímetros de lado
2. Recortamos un cuadrado del material aislante (papel, cartulina…) con un tamaño de unos 7 centímetros de lado (necesitamos que sea más grande que los cuadrados de aluminio)
3. Pegamos a cada lado del cuadrado grande los cuadrados de aluminio procurando que estén lo más centrados posible.

Así de simple es un condensador. ¿Que capacidad tiene nuestro condensador? Para averiguarlo necesitamos conocer:

• La superficie conductora enfrentada (A)
• La distancia entre las superficies conductoras (d)
• La permitividad del material aislante (ε_r)
• La permitividad del vacío ε₀ = 8.8541878176 · 10^-12 F/m

La fórmula del cálculo de la capacitancia del condensador es la siguiente:

En nuestro condensador la superficie conductora es de 5cm * 5cm = 25cm². La distancia entre las superficies conductoras es el grosor del material aislante (un papel normal sería unos 0.15mm). En el caso de haber utilizado papel como dieléctrico la permitividad relativa es de 3.7:

Es decir, nuestro condensador artesanal tiene una capacidad de poco más de 0,5nF, o dicho de otra manera: media milmillonésima parte de Faradio. Los condensadores con más capacidad que se usan habitualmente en las fuentes de alimentación tienen 4.7mF (4.7/1000 Faradios). El Faradio es una unidad “tan grande” que habitualmente se utilizan los micro-Faradios (1/1000000) y los nano-Faradios (1/1000000000).

Para aumentar la capacidad de un condensador podemos:

1. Aumentar la superficie: se puede enrollar el papel permitiendo aumentar la longitud de las tiras de metal-papel-metal. También se puede hacer un apilado de metal-papel-metal-papel-metal uniendo las láminas impares entre si por un lado y las pares por otro.
2. Disminuir la distancia entre las láminas conductoras, pero al hacer el aislante cada vez mas fino soportará menos diferencia de potencial.
3. Utilizar dieléctricos con una alta permitividad.

Dependiendo del tipo de aplicación que se busque se utilizarán unas técnicas u otras. Si se utiliza mica como dieléctrico se apilarán las láminas, puesto que la mica se rompe si se intenta enrollar. Si se necesita que el condensador aguante altas tensiones (100V o más) necesitaremos utilizar mica o poliéster como dieléctrico. En la Wikipedia hay una buena relación de dieléctricos usados y las características y métodos de construcción.

Antes de que se compliquen más las cosas invito a aquellos curiosos que se lean la historia del condensador, un buen resumen en la Wikipedia.

Ahora se van a complicar las cosas

Hora de complicar las cosas, intentaré mantenerme simple y dejaremos las demostraciones matemáticas para otros, pero vamos a analizar el funcionamiento del condensador y considero importante mencionar (que no demostrar) las ecuaciones fundamentales que definen dicho funcionamiento.

Lo primero que tenemos que tener en cuenta es que un condensador almacena carga eléctrica. Podemos decir que almacena energía, por supuesto, pero su funcionamiento es como un recipiente en el que introducimos o sacamos cargas eléctricas. Dichas cargas pueden ser positivas (comúnmente llamadas huecos en electrónica de estado sólido) o negativas (que asociamos directamente con los electrones que son los que realmente se mueven en una corriente eléctrica). En otra ocasión ya explicaré esta dualidad, hoy nos valdrá con pensar en carga eléctrica = electrón.

La carga almacenada en un condensador viene determinada por la siguiente ecuación:

Esta ecuación relaciona la capacidad del condensador (C) con la carga eléctrica (Q) y con la diferencia de potencial entre las placas del condensador (V_c). Si tenemos en cuenta que la corriente eléctrica es:

Podemos relacionar capacidad, tensión y corriente:

Esto es un poco engañoso, porque hemos escrito la capacidad del condensador como si dependiera de la corriente o de la tensión, pero sabemos que la capacidad de un condensador viene determinada únicamente por su construcción y es fija (aunque se pueden construir condensadores de capacidad variable que no vamos a analizar).

Por tanto podemos reformular la anterior ecuación de tres formas distintas:

Si habéis estado atentos habréis advertido que he cambiado la “V” mayúscula de tensión por una “v” minúscula y lo mismo con la corriente. He hecho esto porque estas formulas sólo valen para valores instantáneos, y en electrónica se suelen representar dichos valores instantáneos en minúscula.

Para utilizar las anteriores ecuaciones hay que integrar y diferenciar con la lata que es eso cuando quieres una respuesta rápida. Además el condensador no se comporta igual en corriente continua (la de las pilas y baterías, por ejemplo) o en corriente alterna (la del enchufe).

Circuito básico en corriente continua: RC

El circuito más básico en corriente continua es el RC, también es el más importante.

Una aclaración, en electrónica es común utilizar como símbolo de una tensión la letra “U” en lugar de la “V”, la razón es evitar confundir una variable con el símbolo de Voltio.

Utilizando la ley de Ohm y las leyes de Kirchhoff (aunque estás últimas las podemos sustituir con un poco de sentido común) podemos decir:

Si inicialmente el condensador está descargado, la diferencia de potencial entre sus placas es U_a = 0V. Por tanto vemos que en el instante en el que conectemos al circuito una batería con tensión U_e la corriente que pase por el circuito en ese instante (i = I_o, corriente inicial) dependerá únicamente de la resistencia (R) por lo que podemos decir que virtualmente el condensador descargado es como un cortocircuito en corriente continua. Esto es muy importante, pues es la razón por la cual siempre se suele conectar una resistencia en serie con los condensadores en corriente continua, para limitar la corriente. La única excepción suelen ser las fuentes de alimentación, que tal vez veamos en otra ocasión.

Enseguida nos damos cuenta que según se va cargando el condensador la tensión U_a va a ir aumentando desde los 0V iniciales hasta llegar a igualar a U_e. En ese momento la corriente será nula igual que la tensión de la resistencia U_r.

Demostrar la siguiente ecuación es largo y no lo voy a poner. En corriente continua, para los circuitos de carga y descarga es fundamental. La escribiré en forma de corriente, porque conocida la corriente es fácil calcular los demás parámetros:

Esta ecuación dibuja una curva exponencial. Además podemos calcular fácilmente que cuando t = 5 · R · C la corriente es un 0.7% de la corriente inicial, por lo que se considera el circuito ya estable (cargado o descargado, según el caso). El producto RC se denomina constante de tiempo, se representa por la letra griega tau τ = RC.

En esta simulación la fuente de alimentación cambia cada 10ms de +10V a 0V, con lo que en la práctica tenemos un ciclo de carga de 10ms y un ciclo de descarga de otros 10ms de forma continua. En este sentido cuando la fuente de alimentación está a 0V actúa como un cortocircuito virtual. Al ser la resistencia de 1kΩ y el condensador de un 1μF la constante tau es igual a 1ms. Por tanto el circuito tarda en estabilizarse 5ms.

Condensador en corriente alterna

Si os ha resultado complejo entender el condensador en corriente continua, en corriente alterna es a la vez más complejo y más simple. Matemáticamente suele tender a complicarse bastante, ya que de hecho es indispensable utilizar números complejos, en dónde los electrónicos sustituimos la i del número imaginario por una j por motivos obvios, ya que para nosotros una i siempre es una corriente. Sin embargo, para muchos cálculos basta con imaginar al condensador como una resistencia un tanto particular que denominamos impedancia y representamos por Z en lugar de la habitual R.

Como acabo de decir, en corriente alterna los condensadores se comportan como una “resistencia especial” que denominamos impedancia y representamos con una Z cuyo valor en ohmios es:

Veamos, como la electricidad es física y la física mide los ángulos en radianes lo primero que tenemos que entender es que no podemos expresar la frecuencia de la corriente alterna (los 50Hz del enchufe de nuestras casas si vives en España) en hercios (Hz o ciclos por segundo). Así que tenemos que utilizar la frecuencia angular (aka velocidad angular). La frecuencia angular se representa por la letra griega omega y es ω = 2 · π · f.

Pero vemos que hay una j que como he contado antes representa un número imaginario. Si recordamos los números complejos son la representación matemática de los vectores. Al no tener parte real el vector tiene un ángulo de 90º. En concreto se dice que los condensadores desfasan la corriente de la tensión adelantándola 90º.

Esto último es lo que es realmente interesante de conocer por la persona de a pie porque resulta que las comercializadoras de electricidad lo tienen en cuenta para la factura. El angulo entre la corriente y la tensión se denomina por la letra griega phi (φ) y normalmente nos interesa el coseno de phi (aka factor de potencia). Si dicho coseno es igual a 1 entonces φ = 0 y tenemos una carga resistiva pura. Es lo que las eléctricas nos cobran, la carga resistiva. Resulta que si tenemos muchos motores o fluorescentes estamos añadiendo una gran carga inductiva (los motores tienen bobinas, ya hablaré algún día de ellas) que hace que la corriente se retrase con un angulo de -90º, justo el contrario que los condensadores, por eso en las fábricas suele haber un dispositivo que conecta tanta carga capacitiva (tantos condensadores) como sean necesarios para que el ángulo entre tensión y corriente sea lo más cercano a cero posible. En definitiva hacer que el coseno de phi sea lo más cercano a uno que se pueda.

En general podemos decir que en los hogares no suele haber mucho problema porque la mayoría de electrodomésticos, aunque tengan bobinas, ya tienen sus propios condensadores para corregir el factor de potencia. Pero hay que tener en cuenta que los nuevos contadores son capaces de medir dicho factor, y que si en una instalación doméstica detectan algo fuera de lugar como un factor de potencia por debajo de 0.90 no nos sorprenda que se pongan en contacto con nosotros. En las instalaciones industriales es obligatorio controlar y corregir dicho factor.

No voy a entrar más en profundidad porque ya me he alargado más de lo que quería, es un tema que, aunque interesante, es matemáticamente un lío y no creo que sea plan.

Esta entrada está inspirada (otra vez) en mis comentarios en la Bitácora de Guti en su entrada sobre Los nuevos Casio Batteryless.

­ Actualización (2017-02-11): He añadido unas simulaciones interactivas de los circuitos gracias al trabajo de Paul Falstad que desarrollo el simulador original en Java y de Iain Sharp que lo convirtió a JavaScript.